Second Order Circuits: Difference between revisions
No edit summary |
|||
| (24 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
'''Second order circuits''' are circuits that have two energy storage | '''Second order circuits''' are circuits that have two energy storage elements, resulting in second-order differential equations. | ||
elements, | |||
One application of second order circuits is in timing computers. As we will see, an underdamped RLC circuit can generate a sinusoidal wave. | |||
There are primarily two types of second order circuits: | |||
* Parallel RLC circuits | |||
* Series RLC circuits | |||
each with two responses: | |||
* Natural response (no power source) | |||
* Forced response (has power source) | |||
<math | This page will analyze them and derive some useful equations. | ||
= Parallel RLC Circuits Natural Response = | |||
[[File:Parallel Unforced RLC Circuit.png|thumb|A parallel unforced RLC circuit]] | |||
By KCL, | |||
<math> | |||
\frac{v}{R} + \frac{1}{L} \int_0^t v d\tau | |||
+ I_0 + C \frac{dv}{dt} = 0 | |||
</math> | |||
By differentiating once with respect to | |||
<math>t</math> and rearranging some constants, | |||
<math> | |||
\frac{d^2 v}{dt^2} + \frac{1}{RC} | |||
\frac{dv}{dt} + \frac{v}{LC} = 0 | |||
</math> | |||
we get a ''homogeneous second-order | |||
differential equation'', which has a standard solution that I | |||
will not go into detail. Briefly, it is solved by assuming | |||
<math>v = A e^{st}</math> since derivatives of <math>v</math> | |||
must take the same form to cancel out to zero. | |||
By applying the standard solution, we have | |||
<math> | |||
A e^{st} \left(s^2 + \frac{s}{RC} + \frac{1}{LC} \right) = 0 | |||
</math> | |||
== Characteristic Equation == | |||
The above simplifies to | |||
<math> | |||
s^2 + \frac{s}{RC} + \frac{1}{LC} = 0 | |||
</math> | |||
This is the '''characteristic equation''' of the differential | |||
equation, as the root of the quadratic determines properties | |||
of <math>v(t)</math> | |||
<math> | |||
s_{1,2} = - \frac{1}{2RC} \pm \sqrt{ | |||
\left(\frac{1}{2RC}\right)^2 - \frac{1}{LC}} | |||
= - \alpha \pm \sqrt{\alpha^2 - \omega_0^2} | |||
</math> | |||
where | |||
<math> | |||
\alpha = \frac{1}{2RC} | |||
</math> | |||
and | |||
<math> | |||
\omega_0 = \frac{1}{\sqrt{LC}} | |||
</math> | |||
It can be pretty easily proven that the sum of the two roots is also a solution | |||
<math> | |||
v = A_1 e^{s_1 t} + A_2 e^{s_2 t} | |||
</math> | |||
== Forms == | |||
[[File:Equations for Analyzing the Step Response of Parallel RLC Circuits.png|alt=Equations for Analyzing the Step Response of Parallel RLC Circuits|thumb|Equations for Analyzing the Step Response of Parallel RLC Circuits]] | |||
Depending on the root, there are three forms: | |||
* '''Overdamped''', where there are real, distinct solutions | |||
* '''Underdamped''', where there are complex solutions | |||
* '''Critically damped''', where the solutions are not distinct. | |||
=== Overdamped === | |||
For an overdamped response, we have | |||
<math> | |||
v = A_1 e^{s_1 t} + A_2 e^{s_2 t} | |||
</math> | |||
The A's can be solved by substituting in <math>v(0)</math> and | |||
<math>dv(0) / dt = i_C / C</math> | |||
<math> | |||
v(0) = A_1 + A_2 | |||
</math> | |||
<math> | |||
dv(0)/dt = A_1 s_1 + A_2 s_2 = \frac{1}{C} \left( \frac{-V_0}{R} - I_0 \right) | |||
</math> | |||
=== Underdamped === | |||
For an underdamped response, we have | |||
<math> | |||
s_{1,2} = - \alpha \pm j \omega_d | |||
</math> | |||
where there is damped radian frequency | |||
<math> | |||
\omega_d = \sqrt{w_0^2 - \alpha^2} | |||
</math> | |||
From Euler's identity, the natural response comes to | |||
<math> | |||
v(t) = B_1 e^{-\alpha t} \cos \omega_d t + B_2 e^{-\alpha t} \sin \omega_d t | |||
</math> | |||
The rest is identical to that of overdamped: | |||
<math> | |||
B_1 = V_0 | |||
</math> | |||
<math> | |||
-\alpha B_1 + \omega_d B_2 = \frac{1}{C} \left( \frac{-V_0}{R} - I_0 \right) | |||
</math> | |||
==== Characteristics ==== | |||
Voltage alternates between positive and negative values due to the two | |||
types of energy-storage elements. It's like a mass suspended on a | |||
spring. | |||
The oscillation rate is fixed by <math>\omega_d</math>, which is why it | |||
is called the '''damped radian frequency'''. | |||
The oscillation amplitude decreases exponentially at a rate determined | |||
by <math>\alpha</math>, so it is called the '''damping factor'''. | |||
Notice that when <math>R \neq 0</math>, there is <math>\alpha > 0</math> | |||
and the circuit is damped. | |||
= Series RLC Circuits Natural Response = | |||
[[File:Unforced RLC Circuit.png|thumb|An unforced series RLC circuit]] | |||
Calculations are very similar to that of parallel circuits, so I'll | |||
speed things up. | |||
The second order differential from KVL is | |||
<math> | |||
\frac{d^2 i}{dt^2} + \frac{R}{L} \frac{di}{dt} + \frac{i}{LC} = 0 | |||
</math> | |||
The resulting characteristic equation is | |||
<math> | |||
s^2 + \frac{R}{L}s + \frac{1}{LC} = 0 | |||
</math> | |||
with roots | |||
<math> | |||
s_{1,2} = - \frac{R}{2L} \pm \sqrt{\left( \frac{R}{2L} \right)^2 - | |||
\frac{1}{LC}} = - \alpha \pm \sqrt{\alpha^2 - \omega_0^2} | |||
</math> | |||
with neper frequency <math>\alpha = \frac{R}{2L} rad/s</math> and | |||
resonant radian frequency <math>\omega_0 = \frac{1}{\sqrt{LC}} rad / s</math> | |||
The form equations are identical to parallel, only with different | |||
<math>\alpha</math>: | |||
[[File:Equations for Analyzing the Step Response of Series RLC Circuits.png|thumb|Equations for Analyzing the Step Response of Series RLC Circuits]] | |||
'''Overdamped:''' | |||
<math> | |||
i(t) = A_1 e^{s_1 t} + A_2 e^{s_2 t} | |||
</math> | |||
<math> | |||
A_1 + A_2 = I_0 | |||
</math> | |||
<math> | |||
A_1 s_1 + A_2 s_2 = \frac{1}{L}(-RI_0 - V_0) | |||
</math> | |||
'''Underdamped:''' | |||
<math> | |||
i(t) = B_1 e^{-\alpha t} \cos \omega_d t + B_2 e^{-\alpha t} \sin \omega_d t | |||
</math> | |||
<math> | |||
B_1 = I_0 | |||
</math> | |||
<math> | |||
-\alpha B_1 + \omega_d B_2 = \frac{1}{L} (-RI_0 - V_0) | |||
</math> | |||
'''Critically damped:''' | |||
<math> | |||
i(t) = D_1 t e^{- \alpha t} + D_2 t e^{- \alpha t} | |||
</math> | |||
<math> | |||
D_2 = I_0 | |||
</math> | |||
<math> | |||
D_1 - \alpha D_2 = \frac{1}{L} (-RI_0 - V_0) | |||
</math> | |||
[[Category:Electrical Engineering]] | |||
Latest revision as of 22:26, 8 March 2024
Second order circuits are circuits that have two energy storage elements, resulting in second-order differential equations.
One application of second order circuits is in timing computers. As we will see, an underdamped RLC circuit can generate a sinusoidal wave.
There are primarily two types of second order circuits:
- Parallel RLC circuits
- Series RLC circuits
each with two responses:
- Natural response (no power source)
- Forced response (has power source)
This page will analyze them and derive some useful equations.
Parallel RLC Circuits Natural Response
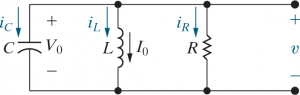
By KCL,
By differentiating once with respect to and rearranging some constants,
we get a homogeneous second-order differential equation, which has a standard solution that I will not go into detail. Briefly, it is solved by assuming since derivatives of must take the same form to cancel out to zero.
By applying the standard solution, we have
Characteristic Equation
The above simplifies to
This is the characteristic equation of the differential equation, as the root of the quadratic determines properties of
where
and
It can be pretty easily proven that the sum of the two roots is also a solution
Forms

Depending on the root, there are three forms:
- Overdamped, where there are real, distinct solutions
- Underdamped, where there are complex solutions
- Critically damped, where the solutions are not distinct.
Overdamped
For an overdamped response, we have
The A's can be solved by substituting in and
Underdamped
For an underdamped response, we have
where there is damped radian frequency
From Euler's identity, the natural response comes to
The rest is identical to that of overdamped:
Characteristics
Voltage alternates between positive and negative values due to the two types of energy-storage elements. It's like a mass suspended on a spring.
The oscillation rate is fixed by , which is why it is called the damped radian frequency.
The oscillation amplitude decreases exponentially at a rate determined by , so it is called the damping factor.
Notice that when , there is and the circuit is damped.
Series RLC Circuits Natural Response
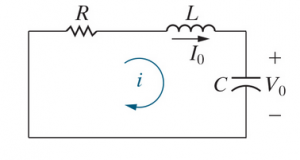
Calculations are very similar to that of parallel circuits, so I'll speed things up.
The second order differential from KVL is
The resulting characteristic equation is
with roots
with neper frequency and resonant radian frequency
The form equations are identical to parallel, only with different :

Overdamped:
Underdamped:
Critically damped:







































