Magnetism: Difference between revisions
No edit summary |
No edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
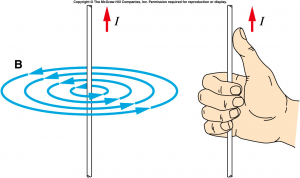
A '''moving charge''' causes a magnetic field, following the right hand | A '''moving charge''' causes a magnetic field, following the right hand | ||
rule: Your thumb pointing towards the direction of movement of the | rule: Your thumb pointing towards the direction of movement of the positive charge, and your other fingers wrap around to indicate the direction of the magnetic field. | ||
positive charge, and your other fingers wrap around to indicate the | |||
direction of the magnetic field. | |||
A circulating current forms a magnetic dipole. | A circulating current forms a magnetic dipole. | ||
| Line 18: | Line 16: | ||
</math> is distance from the wire. | </math> is distance from the wire. | ||
Any component going along the direction of current is cancelled by cross | Any component going along the direction of current is cancelled by cross product. '''Something else'''. Therefore, it is unsurprising that magnetic field is circulating. | ||
product. '''Something else'''. Therefore, it is unsurprising that | |||
magnetic field is circulating. | |||
== | == Straight Line == | ||
Consider a straight line segment starting at <math>z_1</math>and stopping at <math>z_2</math> | |||
= | <math>\vec{B} = \frac{\mu_0 I }{4 \pi \rho} \left( \frac{z_2}{\sqrt{z_2^2 + \rho^2} } - \frac{z_1}{\sqrt{z_1^2 + \rho^2} } \right) \hat{e_\phi}</math> | ||
Let there be a loop of current flowing clockwise. The magnetic field | == Circular Loops == | ||
inside the loop is always going out of the page, whereas the field | |||
outside always go into the page. | Let there be a loop of current flowing clockwise. The magnetic field inside the loop is always going out of the page, whereas the field outside always go into the page. | ||
This can be proven by considering each single length of wire. The shape | This can be proven by considering each single length of wire. The shape | ||
of the loop does not matter. | of the loop does not matter. | ||
A pair of circular loops can produce a very uniform magnetic field in the middle. | |||
=== Solenoid === | |||
'''Solenoids''' use this property to create uniform magnetic fields. They are essentially a long coil of current. Inside the solenoid there is a strong, uniform magnetic field. At the ends, the strength drop drastically. | |||
The field created can be derived from adding together circular loops. | |||
<math> | |||
\vec{B}_{inside, axis} = \mu_0 \frac{N}{L} I \hat{k} | |||
</math> | |||
=== Toroidal Solenoid === | |||
What if we wrap around the solenoid so that they form a loop of coil? we get a circulating magnetic field. The magnitude is the same. | |||
== Rings == | |||
Consider a hollow inner conducting shell inside a hollow outer conducting shell. Run current through the shells and you get a ring of magnetic field. | |||
= Ampere's Law of Magnetic field = | = Ampere's Law of Magnetic field = | ||
| Line 39: | Line 52: | ||
<math> | <math> | ||
\oint_C \vec{B} \cdot d \vec{l} = \mu_0 \iint_{S_L} \vec{J} \cdot d | \oint_C \vec{B} \cdot d \vec{l} = \mu_0 \iint_{S_L} \vec{J} \cdot d | ||
\vec{s} = \mu_0 | \vec{s} = \mu_0 I | ||
</math> | </math> | ||
The general proof of Ampere's Law involves starting from Biot-Savart | The general proof of Ampere's Law involves starting from Biot-Savart Law, integrating to a term and a Maxwell's term. I will do the proof later. | ||
Law, integrating to a term and a Maxwell's term. I will do the proof | |||
later. | [[Category:Physics]] | ||
Latest revision as of 03:28, 5 March 2024
Magnetic Field
A moving charge causes a magnetic field, following the right hand rule: Your thumb pointing towards the direction of movement of the positive charge, and your other fingers wrap around to indicate the direction of the magnetic field.
A circulating current forms a magnetic dipole.
Calculate Field
Where is magnetic permeability, and is distance from the wire.
Any component going along the direction of current is cancelled by cross product. Something else. Therefore, it is unsurprising that magnetic field is circulating.
Straight Line
Consider a straight line segment starting at and stopping at
Circular Loops
Let there be a loop of current flowing clockwise. The magnetic field inside the loop is always going out of the page, whereas the field outside always go into the page.
This can be proven by considering each single length of wire. The shape of the loop does not matter.
A pair of circular loops can produce a very uniform magnetic field in the middle.
Solenoid
Solenoids use this property to create uniform magnetic fields. They are essentially a long coil of current. Inside the solenoid there is a strong, uniform magnetic field. At the ends, the strength drop drastically.
The field created can be derived from adding together circular loops.
Toroidal Solenoid
What if we wrap around the solenoid so that they form a loop of coil? we get a circulating magnetic field. The magnitude is the same.
Rings
Consider a hollow inner conducting shell inside a hollow outer conducting shell. Run current through the shells and you get a ring of magnetic field.
Ampere's Law of Magnetic field
The general proof of Ampere's Law involves starting from Biot-Savart Law, integrating to a term and a Maxwell's term. I will do the proof later.








