Sampling Distribution: Difference between revisions
| (7 intermediate revisions by 2 users not shown) | |||
| Line 29: | Line 29: | ||
# The population distribution of <math>Y</math> is normal, ''or'' | # The population distribution of <math>Y</math> is normal, ''or'' | ||
# The sample size for each <math>Y_i</math> is large <math>n>30</math> | # The sample size for each <math>Y_i</math> is large <math>n>30</math> | ||
By extension, we also have | |||
By extension, we also have the distribution of the sum. | |||
<math>S \sim N(\mu_S = n\mu, \sigma_S = \sqrt{n \sigma})</math> | <math>S \sim N(\mu_S = n\mu, \sigma_S = \sqrt{n \sigma})</math> | ||
where <math>S = \sum Y_i </math> | where <math>S = \sum Y_i </math> | ||
== Proportion Approximation == | |||
The sampling distribution of the proportion of success of ''n'' bernoulli random variables (<math>\hat{p}</math>) can also be approximated to a normal distribution under the CLT. | |||
Consider [[Discrete Random Variable#Bernoulli|bernoulli]] random variables | |||
<math>Y_1 \ldots Y_n \sim E(Y_i) = p, Var(Y_i) = p(1 - p)</math> | |||
The proportion of success <math>\hat{p}</math> is the sum over the count, so the expected probability is | |||
<math>E(\hat{p}) = E \left(\frac{1}{n} \sum Y_i \right) = p</math> | |||
and the variance of <math>\hat{p}</math> is | |||
<math>Var \left(\frac{1}{n} \sum Y_i \right) = \frac{1}{n^2} Var \left(\sum Y_i \right) = \frac{p (1 - p)}{n}</math> | |||
With a large sample size ''n'', we can appoximate this to a normal distribution. Notably, the criteria for a large ''n'' is different from that of the continuous random variable. | |||
<math>np > 5, n(1 - p) > 5</math> | |||
then we have | |||
<math>\hat{p} \sim N \left( p, \frac{p(1-p)}{n} \right)</math> | |||
The reasoning behind the weird criteria relates to the [[Discrete Random Variable|binomial distribution]]. It's not very elaborated on in the lecture, but <math>np</math> is the mean of the binomial (i.e. the expected number of successes). The criteria essentially makes sure that no negative values are plausible in the approximation; with a small mean and a large variance, the left side of a normal approximation goes into the negative, but bernoulli/binomial must always be positive. | |||
== Binomial Approximation == | |||
I'm short on time. This is based on the above section and a bit of math. | |||
<math>Y \sim N(np, np(1 - p))</math> | |||
= Confidence Interval = | = Confidence Interval = | ||
| Line 40: | Line 71: | ||
''(point estimate - margin of error, point estimate + margin of error)'' | ''(point estimate - margin of error, point estimate + margin of error)'' | ||
==== Constructing CIs | == Standard Error == | ||
The '''standard error''' measures how much error we expect to make when estimating <math>\mu_Y</math> by <math>\bar{y}</math>. | |||
== Constructing CIs == | |||
By CLT, <math>\bar{Y} \sim N(\mu, \frac{\sigma^2}{n} )</math>. The | By CLT, <math>\bar{Y} \sim N(\mu, \frac{\sigma^2}{n} )</math>. The | ||
confidence interval is the range of plausible <math>\bar{Y}</math>. | confidence interval is the range of plausible <math>\bar{Y}</math>. | ||
| Line 58: | Line 92: | ||
[[File:T distribution table.png|thumb|T distribution table]] | [[File:T distribution table.png|thumb|T distribution table]] | ||
CLT | CLT is based on the population variance. Since we don't know the population variance <math>\sigma^2</math>, we | ||
Since we don't know the population variance <math>\sigma^2</math>, we | |||
have to use the sample variance <math>s</math> to estimate it. This | have to use the sample variance <math>s</math> to estimate it. This | ||
introduces more uncertainty, accounted for by the '''t-distribution.''' | introduces more uncertainty, accounted for by the '''t-distribution.''' | ||
| Line 110: | Line 141: | ||
I don't really know why. | I don't really know why. | ||
= Sampling Distribution of Difference = | |||
By linear combination of RVs, sampling distribution of <math>\bar{Y_1} - \bar{Y_2}</math> is | |||
<math> | |||
( \bar{Y_1} - \bar{Y_2} ) \sim N(\mu_1 - \mu_2, \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}) | |||
</math> | |||
However, we do not know the population variance <math>\sigma^2</math>. If the CLT assumptions hold, then we have | |||
<math> | |||
\upsilon = \frac{ \left( \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} \right)^2 }{ \frac{(s_1^2 / n_1)^2 }{n_1 - 1} + \frac{(s_2^2 / n_2)^2 }{n_2 - 1} } | |||
</math> | |||
Trust me bro. Remember to round down to use t-table. With this degree of freedom, we can use sample variance to estimate the distribution. | |||
[[Category:Sample Statistics]] | [[Category:Sample Statistics]] | ||
Latest revision as of 17:07, 19 March 2024
Let there be , where each is a randomv variable from the population.
Every Y have the same mean and distribution that we don't know.
We then have the sample mean
The sample mean is expected to be through a pretty easy direct proof
The variance of the sample mean is , also through a pretty easy direct proof.
Central limit theorem
The central limit theorem states that the distribution of the sample mean follows normal distribution.
As long as the following two conditions are satisfied, CLT applies, regardless of the population's distribution.
- The population distribution of is normal, or
- The sample size for each is large
By extension, we also have the distribution of the sum.
where
Proportion Approximation
The sampling distribution of the proportion of success of n bernoulli random variables () can also be approximated to a normal distribution under the CLT.
Consider bernoulli random variables
The proportion of success is the sum over the count, so the expected probability is
and the variance of is
With a large sample size n, we can appoximate this to a normal distribution. Notably, the criteria for a large n is different from that of the continuous random variable.
then we have
The reasoning behind the weird criteria relates to the binomial distribution. It's not very elaborated on in the lecture, but is the mean of the binomial (i.e. the expected number of successes). The criteria essentially makes sure that no negative values are plausible in the approximation; with a small mean and a large variance, the left side of a normal approximation goes into the negative, but bernoulli/binomial must always be positive.
Binomial Approximation
I'm short on time. This is based on the above section and a bit of math.
Confidence Interval
Estimation is the guess for the unknown parameter. A point estimate is a "best guess" of the population parameter, where as the confidence interval is the range of reasonable values that are intended to contain the parameter of interest with a certain degree of confidence, calculated with
(point estimate - margin of error, point estimate + margin of error)
Standard Error
The standard error measures how much error we expect to make when estimating by .
Constructing CIs
By CLT, . The confidence interval is the range of plausible .
If we define the middle 90% to be plausible, to find the confidence interval, simply find the 5th and 95th percentile.
Generalized, if we want a confidence interval of the middle , have a confidence interval of
where is the sample mean and is the z score of the x-th percentile.
T-Distribution
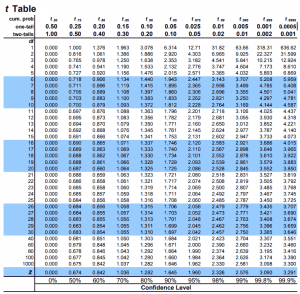
CLT is based on the population variance. Since we don't know the population variance , we have to use the sample variance to estimate it. This introduces more uncertainty, accounted for by the t-distribution.
T-distribution is the distribution of sample mean based on population mean, sample variance and degrees of freedom (covered later). It looks very similar to normal distribution.
When the sample size is small, there is greater uncertainty in the estimates. T-di
The spread of t-distribution depends on the degrees of freedom, which is based on sample size. When looking up the table, round down df.
As the sample size increases, degrees of freedom increase, the spread of t-distribution decreases, and t-distribution approaches normal distribution.
Based on CLT and normal distribution, we had the confidence interval
Now, based on T-distribution, we have the CI
Find Sample Size
To calculate sample size needed depending on desired error margin and sample variance by assuming that
We want to always round up to stay within the error margin.
I don't really know why.
Sampling Distribution of Difference
By linear combination of RVs, sampling distribution of is
However, we do not know the population variance . If the CLT assumptions hold, then we have
Trust me bro. Remember to round down to use t-table. With this degree of freedom, we can use sample variance to estimate the distribution.





































