Adder: Difference between revisions
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
The ''' | The '''adder''' circuit is the fundamental [[Instructions (Computer Science)|instruction]] of many arithmetic operations (such as subtract, multiply, divide, and modulo). | ||
= | = Half and full adder = | ||
ADD takes in two binary digits. It then outputs the result, which consists of a digit and a carry. | |||
In contrast to the above, which is a '''half adder''', a '''full adder''' has an additional input: '''carry-in''', which modifies the result. | In contrast to the above, which is a '''half adder''', a '''full adder''' has an additional input: '''carry-in''', which modifies the result. | ||
Full adders can be constructed with two half adders. | Full adders can be constructed with two half adders. | ||
== Ripple carry adder | == Circuit == | ||
A '''ripple carry adder''' is constructed with multiple full adders to | [[File:Full adder.png|thumb|Figure 1.]] | ||
Consider full adder that performs A + B = Y with carry-in and carry-out. After simplification with truth table and boolean algebra, we have | |||
<math>Y = (A\oplus B)\oplus C</math> | |||
<math>C_{in}=AB+(A\oplus B)C</math> | |||
with circuit shown in Figure 1. | |||
= Subtraction = | |||
The adder circuit can be used for subtraction without many changes. Simply negate the subtracted input, add a carry-in, and perform addition. | |||
The principle behind this is [[two's complement]]. | |||
= Ripple carry adder = | |||
A '''ripple carry adder''' is constructed with multiple full adders, linking each one's carry-out to the next's carry-in. It is capable of computing multi-digit addition. Each full adder contributes some propagation delay due to the need to input carry to the next full adder. | |||
= Carry look-ahead adder = | |||
Some optimization can be done to make the ripple carry adder circuit more parallel for a faster propagation delay. | |||
A ''generate'' signal is ab. A ''propagate'' signal is a XOR b. Rewriting sum and carry in those terms can make the circuit more parallel | |||
<math> | |||
S_i=P_i \oplus C_{i-1} | |||
</math> | |||
<math> | |||
C_i=q_i+P_iC_{i-1} | |||
</math> | |||
== Overflow detection == | |||
Consider two signed integers being operated on by our ripple carry adder. If there is an overflow, the last carry-in should be different from the first carry-out. Try proving it case by case. I gotta go do my machine learning lab now bye. | |||
[[Category:Computer Architecture]][[Category:ECS154A Midterm]] | [[Category:Computer Architecture]][[Category:ECS154A Midterm]] | ||
Latest revision as of 15:35, 13 May 2024
The adder circuit is the fundamental instruction of many arithmetic operations (such as subtract, multiply, divide, and modulo).
Half and full adder
ADD takes in two binary digits. It then outputs the result, which consists of a digit and a carry.
In contrast to the above, which is a half adder, a full adder has an additional input: carry-in, which modifies the result.
Full adders can be constructed with two half adders.
Circuit
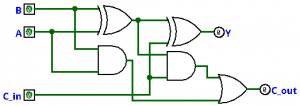
Consider full adder that performs A + B = Y with carry-in and carry-out. After simplification with truth table and boolean algebra, we have
with circuit shown in Figure 1.
Subtraction
The adder circuit can be used for subtraction without many changes. Simply negate the subtracted input, add a carry-in, and perform addition.
The principle behind this is two's complement.
Ripple carry adder
A ripple carry adder is constructed with multiple full adders, linking each one's carry-out to the next's carry-in. It is capable of computing multi-digit addition. Each full adder contributes some propagation delay due to the need to input carry to the next full adder.
Carry look-ahead adder
Some optimization can be done to make the ripple carry adder circuit more parallel for a faster propagation delay.
A generate signal is ab. A propagate signal is a XOR b. Rewriting sum and carry in those terms can make the circuit more parallel
Overflow detection
Consider two signed integers being operated on by our ripple carry adder. If there is an overflow, the last carry-in should be different from the first carry-out. Try proving it case by case. I gotta go do my machine learning lab now bye.




