Magnetism

Magnetic Field

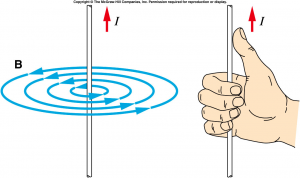
A moving charge causes a magnetic field, following the right hand rule: Your thumb pointing towards the direction of movement of the positive charge, and your other fingers wrap around to indicate the direction of the magnetic field.

A circulating current forms a magnetic dipole.

Calculate Field

Magnetic field of a current with right hand rule

${\vec {B}}({\vec {r}})={\frac {\mu _{0}}{4\pi }}{\frac {I_{1}d{\vec {l}}_{1}\times {\hat {r}}}{r^{2}}}={\frac {\mu _{0}}{4\pi }}{\frac {\left|Idl\right|}{r^{3}}}\rho {\hat {e}}_{\phi }$

Where $\mu _{0}$ is magnetic permeability, and $\rho$ is distance from the wire.

Any component going along the direction of current is cancelled by cross product. Something else. Therefore, it is unsurprising that magnetic field is circulating.

Special Field: Wire

- TODO: Later fill out <01-03-24, xydxydxyd1> -

Loops

Let there be a loop of current flowing clockwise. The magnetic field inside the loop is always going out of the page, whereas the field outside always go into the page.

This can be proven by considering each single length of wire. The shape of the loop does not matter.

Ampere's Law of Magnetic field

$\oint _{C}{\vec {B}}\cdot d{\vec {l}}=\mu _{0}\iint _{S_{L}}{\vec {J}}\cdot d{\vec {s}}=\mu _{0}i$

The general proof of Ampere's Law involves starting from Biot-Savart Law, integrating to a term and a Maxwell's term. I will do the proof later.