Second Order Circuits

Second order circuits are circuits that have two energy storage elements, resulting in second-order differential equations.

One application of second order circuits is in timing computers. As we will see, an RLC circuit can generate a sinusoidal wave.

There are primarily two types of second order circuits:

• Parallel RLC circuits
• Series RLC circuits

Series RLC Circuits

Natural Response

An unforced series RLC circuit

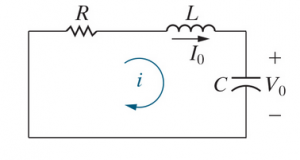
Consider an un-forced RLC circuit. We want to find $V_{C}$.

First, we can use KVL and KCL

$V_{R}+V_{L}+V_{C}=0$

$iR+L{\frac {di}{dt}}+V_{C}=0$

Next, we can use $i=C{\frac {dV_{C}}{dt}}$ and substitution to get

$RC{\frac {dV_{C}}{dt}}+L{\frac {d}{dt}}{\frac {CV_{C}}{dt}}V_{C}=0$

Changing the order and moving the constants,

$LC{\frac {d^{2}V}{dt^{2}}}+RC{\frac {dV_{C}}{dt}}+V_{C}=0$

Moving constants away from the first term to get a second-order differential equation,

${\frac {d^{2}V_{C}}{dt^{2}}}+{\frac {R}{L}}{\frac {dV_{C}}{dt}}+{\frac {1}{LC}}V_{C}=0$

Parallel RLC Circuits

Natural Response

A parallel unforced RLC circuit

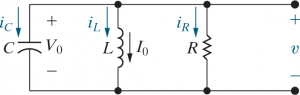
By KCL,

${\frac {v}{R}}+{\frac {1}{L}}\int _{0}^{t}vd\tau +I_{0}+C{\frac {dv}{dt}}=0$

By differentiating once with respect to $t$ and rearranging some constants,

${\frac {d^{2}v}{dt^{2}}}+{\frac {1}{RC}}{\frac {dv}{dt}}+{\frac {v}{LC}}=0$

we get a homogeneous second-order differential equation.