Bivariate: Difference between revisions
No edit summary |
|||
| Line 66: | Line 66: | ||
== Regression Effect == | == Regression Effect == | ||
[[File:Regression Effect Scatter Plot.png|thumb|Regression effect demonstrated by SD line and Regression line]] | |||
The '''regression effect''' is the phenomenon that the best prediction | The '''regression effect''' is the phenomenon that the best prediction | ||
of <math>Y</math> given <math>X = x</math> is less rare for | of <math>Y</math> given <math>X = x</math> is less rare for | ||
Revision as of 18:28, 18 March 2024
Consider two numerica random variables and . We can measure their covariance.
The correlation of two random variables measures the line dependent between and
Correlation is always between -1 and 1
Bivariate Normal
The bivariate normal (aka. bivariate gaussian) is one special type of continuous random variable.
is bivariate normal if
- The marginal PDF of both X and Y are normal
- For any , the condition PDF of given is Normal
- Works the other way around: Bivariate gaussian means that condition is satisfied
Predicting Y given X
Given bivariate normal, we can predict one variable given another. Let us try estimating the expected Y given X is x
There are three main methods
- Scatter plot approximation
- Joint PDF
- 5 statistics
5 Parameters
We need to know 5 parameters about and
If follows bivariate normal distribution, then we have
The left side is the predicted Z-score for Y, and the right side is the product of correlation and Z-score of X = x
The variance is given by
Due to the range of , the variance of Y given X is always smaller than the actual variance. The standard deviation is just rooted that.
Regression Effect
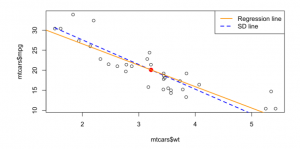
The regression effect is the phenomenon that the best prediction of given is less rare for than ; Future predictions regress to mediocrity.
When you plot all the predicted , you get the linear regression line. The regression effect can be demonstrated by also plotting the SD line (where the correlation is not applied).













