Bivariate

Consider two numerica random variables $X$ and $Y$. We can measure their covariance.

$Cov(X,Y)$

The correlation of two random variables measures the line dependent between $X$ and $Y$

$Cor(X,Y)=\rho ={\frac {Cov(X,Y)}{sd(X)sd(Y)}}$

Correlation is always between -1 and 1

Bivariate Normal

The bivariate normal (aka. bivariate gaussian) is one special type of continuous random variable.

$(X,Y)$ is bivariate normal if

1. The marginal PDF of both X and Y are normal
2. For any $x$, the condition PDF of $Y$ given $X=x$ is Normal

• • Works the other way around: Bivariate gaussian means that condition is satisfied

Predicting Y given X

Given bivariate normal, we can predict one variable given another. Let us try estimating the expected Y given X is x

$E(Y|X=x)$

There are three main methods

• Scatter plot approximation
• Joint PDF
• 5 statistics

5 Parameters

We need to know 5 parameters about $X$ and $Y$

$E(X),sd(X),E(Y),sd(Y),\rho$

If $X,Y$ follows bivariate normal distribution, then we have

$\left({\frac {E(Y|X=x)-E(Y)}{sd(Y)}}\right)=\rho \left({\frac {x-E(X)}{sd(X)}}\right)$

The left side is the predicted Z-score for Y, and the right side is the product of correlation and Z-score of X = x

The variance is given by

$Var(Y|X=x)=(1-\rho ^{2})Var(Y)$

Due to the range of $\rho$, the variance of Y given X is always smaller than the actual variance. The standard deviation is just rooted that.

Regression Effect

Regression effect demonstrated by SD line and Regression line

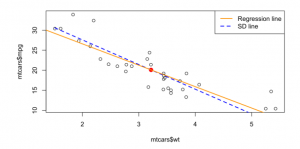
The regression effect is the phenomenon that the best prediction of $Y$ given $X=x$ is less rare for $Y$ than $x$; Future predictions regress to mediocrity.

When you plot all the predicted $E(Y|X=x)$, you get the linear regression line. The regression effect can be demonstrated by also plotting the SD line (where the correlation is not applied).

Linear Regression

$y_{i}=\beta _{0}+\beta _{1}x_{i}+\epsilon _{i}$

where the $\beta _{0},\beta _{1}$ are regression coefficients (slope, intercept) based on the population, and $\epsilon _{i}$ is error for the i-th subject.

We want to estimate the regression coefficients.

Let ${\hat {y_{i}}}$ be an estimation of $y_{i}$; a prediction at $X=x$, with

${\hat {y_{i}}}={\hat {\beta _{0}}}+{\hat {\beta _{1}}}x_{i}$

We can measure the vertical error $e_{i}=y_{i}-{\hat {y_{i}}}$

The overall error is the sum of squared errors $SSE=\sum _{i}^{n}e_{i}^{2}$. The best fit line is the line minimizing SSE.

Using calculus, we can find that the line has the following scope and intercept:

${\hat {\beta _{1}}}=r{\frac {s_{y}}{s_{x}}}$

where $r$ is the strength of linear relationship, and $s_{x},s_{y}$ is the deviations of the sample. They are basically the sample versions of $\rho ,\sigma$

${\hat {\beta _{0}}}={\bar {Y}}-{\hat {\beta _{1}}}{\bar {X}}$

Interpretation

$\beta _{1}$ (the slope) is the estimated change in $Y$ when $X$ changes by one unit.

$\beta _{0}$ (the intercept) is the estimated average of $Y$ when $X=0$. If $X$ cannot be 0, this may not have a practical meaning.

$r^{2}$ (coefficient of determination) measures how good the line fits the data.

$r^{2}={\frac {\sum ({\hat {y_{i}}}-{\bar {Y}})^{2}}{\sum (y_{i}-{\bar {Y}})^{2}}}$

The bottom is total variance. The top is reduced. The value is the proportion of variance in $y$ that is explained by the linear relationship between $X$ and $Y$.