Logistic regression: Difference between revisions
From Rice Wiki
(Created page with "= Linear regression = Linear regression cannot be directly used for (binary) classification. Indirectly, a threshold is used. When the value is above the threshold, it is considered 1; when it is below, it is considered 0. Classification using linear regression is sensitive to the threshold. The problem with this approach is the difficulty in determining a good threshold.") |
No edit summary |
||
| Line 1: | Line 1: | ||
[[File:Logistic regression sigmoid.png|thumb|Figure 1. The shape of the logistic regression function is an S]] | |||
'''Logistic regression''' uses the logistic function (sigmoid) to map the output of a linear regression function <math>z</math> to 0 or 1. | |||
= Linear regression = | = Linear regression = | ||
Linear regression cannot be directly used for (binary) classification. Indirectly, a threshold is used. When the value is above the threshold, it is considered 1; when it is below, it is considered 0. | Linear regression cannot be directly used for (binary) classification. Indirectly, a threshold is used. When the value is above the threshold, it is considered 1; when it is below, it is considered 0. | ||
Classification using linear regression is sensitive to the threshold. The problem with this approach is the difficulty in determining a good threshold. | Classification using linear regression is sensitive to the threshold. The problem with this approach is the difficulty in determining a good threshold. Logistic regression mitigates that by feeding <math>z</math> into a logistic function. | ||
= Logistic function = | |||
As shown in figure 1, the sigmoid is S-shaped. It is a good approximation of the transition from 0 to 1. | |||
As stated in the last section, we feed the output of linear regression into sigmoid. | |||
<math> | |||
sigm(z=wx)=\frac{1}{1+e^{-z}} | |||
</math> | |||
Revision as of 01:23, 26 April 2024
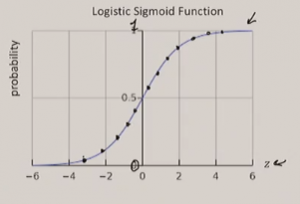
Logistic regression uses the logistic function (sigmoid) to map the output of a linear regression function to 0 or 1.
Linear regression
Linear regression cannot be directly used for (binary) classification. Indirectly, a threshold is used. When the value is above the threshold, it is considered 1; when it is below, it is considered 0.
Classification using linear regression is sensitive to the threshold. The problem with this approach is the difficulty in determining a good threshold. Logistic regression mitigates that by feeding into a logistic function.
Logistic function
As shown in figure 1, the sigmoid is S-shaped. It is a good approximation of the transition from 0 to 1.
As stated in the last section, we feed the output of linear regression into sigmoid.


