Perceptron learning: Difference between revisions
From Rice Wiki
(Created page with "'''Perceptron learning''' is good for classifying ''linearly separable data'', as seen in figure 1. Category:Machine Learning") |
No edit summary |
||
| Line 1: | Line 1: | ||
'''Perceptron learning''' is good for classifying ''linearly separable data'', as seen in figure 1. | [[File:Linearly separable data.png|thumb|Figure 1. Graphical representation of linearly separable data]] | ||
'''Perceptron learning''' is an algorithm for [[binary classification]]. It is good for classifying ''linearly separable data'', as seen in figure 1. | |||
= How it works = | |||
Initially, all attributes are passed into a ''neuron'', each with a randomized weight. | |||
<math>z = \bf{w}\bf{x}</math> | |||
The '''binary step activation function''' takes in z and outputs 1 or 0 depending on a ''threshold''. | |||
The error is computed | |||
<math>E = \frac{1}{2} \sum (y^{(i)} - \hat{y}^{(i)})^2</math> | |||
where the 1/2 is for simplicity of computation after the gradient. We use the gradient of the error function to update the weights of the model | |||
<math>\Delta w_j = \nabla_{w_j} E = \sum (y^{(i)} - \hat{y^{(i)}})(-x_j)</math> | |||
[[Category:Machine Learning]] | [[Category:Machine Learning]] | ||
Revision as of 06:03, 26 April 2024
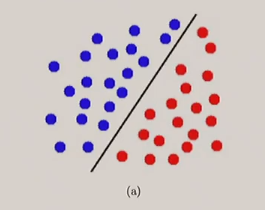
Perceptron learning is an algorithm for binary classification. It is good for classifying linearly separable data, as seen in figure 1.
How it works
Initially, all attributes are passed into a neuron, each with a randomized weight.
The binary step activation function takes in z and outputs 1 or 0 depending on a threshold.
The error is computed
where the 1/2 is for simplicity of computation after the gradient. We use the gradient of the error function to update the weights of the model



