Adder

The adder circuit is the fundamental instruction of many arithmetic operations (such as subtract, multiply, divide, and modulo).

Half and full adder

ADD takes in two binary digits. It then outputs the result, which consists of a digit and a carry.

In contrast to the above, which is a half adder, a full adder has an additional input: carry-in, which modifies the result.

Full adders can be constructed with two half adders.

Circuit

Figure 1.

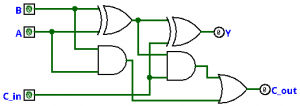
Consider full adder that performs A + B = Y with carry-in and carry-out. After simplification with truth table and boolean algebra, we have

$Y=(A\oplus B)\oplus C$

$C_{in}=AB+(A\oplus B)C$

with circuit shown in Figure 1.

Subtraction

The adder circuit can be used for subtraction without many changes. Simply negate the subtracted input, add a carry-in, and perform addition.

The principle behind this is two's complement.

Ripple carry adder

A ripple carry adder is constructed with multiple full adders, linking each one's carry-out to the next's carry-in. It is capable of computing multi-digit addition. Each full adder contributes some propagation delay due to the need to input carry to the next full adder.