Second Order Circuits: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
'''Second order circuits''' are circuits that have two energy storage | '''Second order circuits''' are circuits that have two energy storage | ||
elements, resultingin second-order differential equations. The circuits have to be cast in terms of irreducible elements (i.e. | elements, resultingin second-order differential equations. The circuits have to be cast in terms of irreducible elements (i.e. combine L's and C's into one when possible).[[File:Unforced RLC Circuit.png|thumb|An unforced RLC circuit]] | ||
combine L's and C's into one when possible).[[File:Unforced RLC Circuit.png|thumb|An unforced RLC circuit]] | |||
Consider an un-forced RLC circuit. We want to find <math>V_C</math>. | Consider an un-forced RLC circuit. We want to find <math>V_C</math>. | ||
| Line 12: | Line 11: | ||
Next, we can use <math>i = C \frac{dV_C}{dt}</math> to get | Next, we can use <math>i = C \frac{dV_C}{dt}</math> to get | ||
<math | <math>RC \frac{dV_C}{dt} + L \frac{d}{dt} \frac{C V_C} {dt} V_C = 0</math> | ||
<math>LC \frac{d^2 V}{dt^2} + RC \frac{dV_C}{dt} + V_C = 0</math> | |||
<math>\frac{d^2V_C}{dt^2} + \frac{R}{L} \frac{dV_C}{dt} + \frac{1}{LC} V_C = 0</math> | |||
The above is a ''second-order differential equation!'' We have ways to solve that. | |||
Revision as of 03:43, 1 March 2024
Second order circuits are circuits that have two energy storage
elements, resultingin second-order differential equations. The circuits have to be cast in terms of irreducible elements (i.e. combine L's and C's into one when possible).
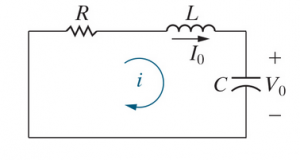
Consider an un-forced RLC circuit. We want to find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_C} .
First, we can use KVL and KCL
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_R + V_L + V_C = 0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle iR + L \frac{di}{dt} + V_C = 0}
Next, we can use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = C \frac{dV_C}{dt}} to get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle RC \frac{dV_C}{dt} + L \frac{d}{dt} \frac{C V_C} {dt} V_C = 0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LC \frac{d^2 V}{dt^2} + RC \frac{dV_C}{dt} + V_C = 0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2V_C}{dt^2} + \frac{R}{L} \frac{dV_C}{dt} + \frac{1}{LC} V_C = 0}
The above is a second-order differential equation! We have ways to solve that.
