Second Order Circuits: Difference between revisions
From Rice Wiki
| Line 36: | Line 36: | ||
== Natural Response == | == Natural Response == | ||
[[File:Parallel Unforced RLC Circuit.png|thumb|A parallel unforced RLC circuit]] | [[File:Parallel Unforced RLC Circuit.png|thumb|A parallel unforced RLC circuit]] | ||
By KCL, | |||
<math> | |||
\frac{v}{R} + \frac{1}{L} \int_0^t v d\tau | |||
+ I_0 + C \frac{dv}{dt} = 0 | |||
</math> | |||
By differentiating once with respect to | |||
<math>t</math> and rearranging some constants, | |||
<math> | |||
\frac{d^2 v}{dt^2} + \frac{1}{RC} | |||
\frac{dv}{dt} + \frac{v}{LC} = 0 | |||
</math> | |||
we get a ''homogeneous second-order | |||
differential equation''. | |||
[[Category:Electrical Engineering]] | [[Category:Electrical Engineering]] | ||
Revision as of 07:29, 8 March 2024
Second order circuits are circuits that have two energy storage elements, resulting in second-order differential equations.
One application of second order circuits is in timing computers. As we will see, an RLC circuit can generate a sinusoidal wave.
There are primarily two types of second order circuits:
- Parallel RLC circuits
- Series RLC circuits
Series RLC Circuits
Natural Response
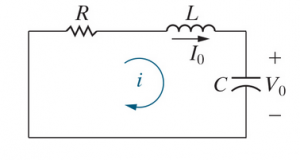
Consider an un-forced RLC circuit. We want to find .
First, we can use KVL and KCL
Next, we can use and substitution to get
Changing the order and moving the constants,
Moving constants away from the first term to get a second-order differential equation,
Parallel RLC Circuits
Natural Response
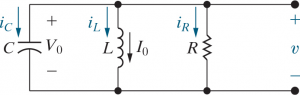
By KCL,
By differentiating once with respect to and rearranging some constants,
we get a homogeneous second-order differential equation.










