Second Order Circuits

Second order circuits are circuits that have two energy storage elements, resulting in second-order differential equations.

One application of second order circuits is in timing computers. As we will see, an RLC circuit can generate a sinusoidal wave.

There are primarily two types of second order circuits:

• Parallel RLC circuits
• Series RLC circuits

This page will analyze them and derive some useful equations.

Series RLC Circuits

Natural Response

An unforced series RLC circuit

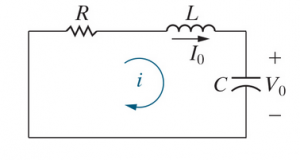
Consider an un-forced RLC circuit. We want to find $V_{C}$.

First, we can use KVL and KCL

$V_{R}+V_{L}+V_{C}=0$

$iR+L{\frac {di}{dt}}+V_{C}=0$

Next, we can use $i=C{\frac {dV_{C}}{dt}}$ and substitution to get

$RC{\frac {dV_{C}}{dt}}+L{\frac {d}{dt}}{\frac {CV_{C}}{dt}}V_{C}=0$

Changing the order and moving the constants,

$LC{\frac {d^{2}V}{dt^{2}}}+RC{\frac {dV_{C}}{dt}}+V_{C}=0$

Moving constants away from the first term to get a second-order differential equation,

${\frac {d^{2}V_{C}}{dt^{2}}}+{\frac {R}{L}}{\frac {dV_{C}}{dt}}+{\frac {1}{LC}}V_{C}=0$

Parallel RLC Circuits

Natural Response

A parallel unforced RLC circuit

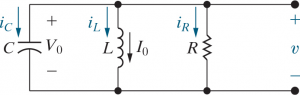
By KCL,

${\frac {v}{R}}+{\frac {1}{L}}\int _{0}^{t}vd\tau +I_{0}+C{\frac {dv}{dt}}=0$

By differentiating once with respect to $t$ and rearranging some constants,

${\frac {d^{2}v}{dt^{2}}}+{\frac {1}{RC}}{\frac {dv}{dt}}+{\frac {v}{LC}}=0$

we get a homogeneous second-order differential equation, which has a standard solution that I will not go into detail. Briefly, it is solved by assuming $v=Ae^{st}$ since derivatives of $v$ must take the same form to cancel out to zero.

By applying the standard solution, we have

$Ae^{st}\left(s^{2}+{\frac {s}{RC}}+{\frac {1}{LC}}\right)=0$

Which simplifies to

$s^{2}+{\frac {s}{RC}}+{\frac {1}{LC}}=0$

This is the characteristic equation of the differential equation, as the root of the quadratic determines properties of $v(t)$

$s_{1,2}=-{\frac {1}{2RC}}\pm {\sqrt {\left({\frac {1}{2RC}}\right)^{2}-{\frac {1}{LC}}}}=-\alpha \pm {\sqrt {\alpha ^{2}-\omega _{0}^{2}}}$

where

$\alpha ={\frac {1}{2RC}}$

and

$\omega _{0}={\frac {1}{\sqrt {LC}}}$

It can be pretty easily proven that the sum of the two roots is also a solution

$v=A_{1}e^{s_{1}t}+A_{2}e^{s_{2}t}$