Second Order Circuits

Second order circuits are circuits that have two energy storage elements, resulting in second-order differential equations.

One application of second order circuits is in timing computers. As we will see, an RLC circuit can generate a sinusoidal wave.

There are primarily two types of second order circuits:

• Parallel RLC circuits
• Series RLC circuits

This page will analyze them and derive some useful equations.

Series RLC Circuits

Natural Response

An unforced series RLC circuit

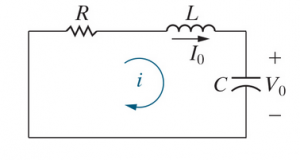
Consider an un-forced RLC circuit. We want to find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_C} .

First, we can use KVL and KCL

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_R + V_L + V_C = 0}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle iR + L \frac{di}{dt} + V_C = 0}

Next, we can use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = C \frac{dV_C}{dt}} and substitution to get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle RC \frac{dV_C}{dt} + L \frac{d}{dt} \frac{C V_C} {dt} V_C = 0}

Changing the order and moving the constants,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LC \frac{d^2 V}{dt^2} + RC \frac{dV_C}{dt} + V_C = 0}

Moving constants away from the first term to get a second-order differential equation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2V_C}{dt^2} + \frac{R}{L} \frac{dV_C}{dt} + \frac{1}{LC} V_C = 0}

Parallel RLC Circuits

Natural Response

A parallel unforced RLC circuit

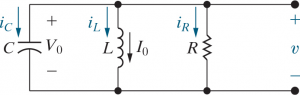
By KCL,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{v}{R} + \frac{1}{L} \int_0^t v d\tau + I_0 + C \frac{dv}{dt} = 0 }

By differentiating once with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} and rearranging some constants,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2 v}{dt^2} + \frac{1}{RC} \frac{dv}{dt} + \frac{v}{LC} = 0 }

we get a homogeneous second-order differential equation, which has a standard solution that I will not go into detail. Briefly, it is solved by assuming Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v = A e^{st}} since derivatives of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} must take the same form to cancel out to zero.

By applying the standard solution, we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A e^{st} \left(s^2 + \frac{s}{RC} + \frac{1}{LC} \right) = 0 }

Characteristic Equation

The above simplifies to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s^2 + \frac{s}{RC} + \frac{1}{LC} = 0 }

This is the characteristic equation of the differential equation, as the root of the quadratic determines properties of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(t)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{1,2} = - \frac{1}{2RC} \pm \sqrt{ \left(\frac{1}{2RC}\right)^2 - \frac{1}{LC}} = - \alpha \pm \sqrt{\alpha^2 - \omega_0^2} }

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = \frac{1}{2RC} }

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0 = \frac{1}{\sqrt{LC}} }

It can be pretty easily proven that the sum of the two roots is also a solution

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v = A_1 e^{s_1 t} + A_2 e^{s_2 t} }

Forms

Depending on the root, there are three forms:

• Overdamped, where there are real, distinct solutions
• Underdamped, where there are complex solutions
• Critically damped, where the solutions are not distinct.

Overdamped

For an overdamped response, we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v = A_1 e^{s_1 t} + A_2 e^{s_2 t} }

The A's can be solved by substituting in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(0)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dv(0) / dt = i_C / C}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(0) = A_1 + A_2 }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dv(0)/dt = A_1 s_1 + A_2 s_2 = \frac{1}{C} \left( \frac{-V_0}{R} - I_0 \right) }

Underdamped

For an underdamped response, we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_{1,2} = - \alpha \pm j \omega_d }

where there is damped radian frequency

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_d = \sqrt{w_0^2 - \alpha^2} }

From Euler's identity, the natural response comes to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v(t) = B_1 e^{-\alpha t} \cos \omega_d t + B_2 e^{-\alpha t} \sin \omega_d t }

The rest is identical to that of overdamped:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_1 = V_0 }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\alpha B_1 + \omega_d B_2 = \frac{1}{C} \left( \frac{-V_0}{R} - I_0 \right) }

Characteristics

Voltage alternates between positive and negative values due to the two types of energy-storage elements. It's like a mass suspended on a spring.

The oscillation rate is fixed by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_d} , which is why it is called the damped radian frequency.

The oscillation amplitude decreases exponentially at a rate determined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} , so it is called the damping factor.

Notice that when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R \neq 0} , there is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha > 0} and the circuit is damped.