Sampling Distribution: Difference between revisions
(Created page with "= Sampling distribution = Let there be <math>Y_1, Y_2, \ldots, Y_n </math>, where each <math>Y_i</math> is a randomv variable from the population. Every Y have the same mean and distribution that we don't know. <math> E(Y_i) = \mu, Var(Y_i) = \sigma^2 </math> We then have the sample mean <math> \bar{Y} = \frac{1}{n} \sum_{i = 1}^n Y_i </math> The sample mean is expected to be <math>\mu</math> through a pretty easy direct proof The variance of the sample mean is <ma...") |
No edit summary |
||
| Line 1: | Line 1: | ||
Let there be <math>Y_1, Y_2, \ldots, Y_n </math>, where each | Let there be <math>Y_1, Y_2, \ldots, Y_n </math>, where each | ||
<math>Y_i</math> is a randomv variable from the population. | <math>Y_i</math> is a randomv variable from the population. | ||
| Line 21: | Line 20: | ||
through a pretty easy direct proof. | through a pretty easy direct proof. | ||
= Central limit theorem = | |||
The '''central limit theorem''' states that the distribution of the sample mean follows normal distribution. | The '''central limit theorem''' states that the distribution of the sample mean follows normal distribution. | ||
Revision as of 01:38, 12 March 2024
Let there be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_1, Y_2, \ldots, Y_n } , where each Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_i} is a randomv variable from the population.
Every Y have the same mean and distribution that we don't know.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E(Y_i) = \mu, Var(Y_i) = \sigma^2 }
We then have the sample mean
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{Y} = \frac{1}{n} \sum_{i = 1}^n Y_i }
The sample mean is expected to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} through a pretty easy direct proof
The variance of the sample mean is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\sigma^2}{n}} , also through a pretty easy direct proof.
Central limit theorem
The central limit theorem states that the distribution of the sample mean follows normal distribution.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{Y} \sim N(\mu, \frac{\sigma^2}{n})}
As long as the following two conditions are satisfied, CLT applies, regardless of the population's distribution.
- The population distribution of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} is normal, or
- The sample size for each Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_i} is large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n>30}
By extension, we also have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S \sim N(\mu_S = n\mu, \sigma_S = \sqrt{n \sigma})}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S = \sum Y_i }
Confidence Interval
Estimation is the guess for the unknown parameter. A point estimate is a "best guess" of the population parameter, where as the confidence interval is the range of reasonable values that are intended to contain the parameter of interest with a certain degree of confidence, calculated with
(point estimate - margin of error, point estimate + margin of error)
Constructing CIs
By CLT, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{Y} \sim N(\mu, \frac{\sigma^2}{n} )} . The confidence interval is the range of plausible Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{Y}} .
If we define the middle 90% to be plausible, to find the confidence interval, simply find the 5th and 95th percentile.
Generalized, if we want a confidence interval of the middle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1 - \alpha) 100%} , have a confidence interval of
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{y} \pm Z_{\alpha / 2} \frac{\sigma}{ \sqrt{n} } }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{y}} is the sample mean and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{x}} is the z score of the x-th percentile.
T-Distribution
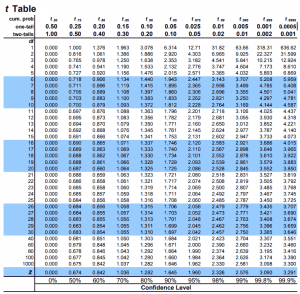
CLT has several restrictions, the biggest one being a large sample size. T-
Since we don't know the population variance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma^2} , we have to use the sample variance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} to estimate it. This introduces more uncertainty, accounted for by the t-distribution.
T-distribution is the distribution of sample mean based on population mean, sample variance and degrees of freedom (covered later). It looks very similar to normal distribution.
When the sample size Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} is small, there is greater uncertainty in the estimates. T-di
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{\alpha/2} > Z_{\alpha/2} }
The spread of t-distribution depends on the degrees of freedom, which is based on sample size
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upsilon = n - 1 }
As the sample size increases, degrees of freedom increase, the spread of t-distribution decreases, and t-distribution approaches normal distribution.
Based on CLT and normal distribution, we had the confidence interval
Now, based on T-distribution, we have the CI
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{Y} \pm t_{\alpha / 2} \frac{s}{ \sqrt{n} } }
Find Sample Size
To calculate sample size needed depending on desired error margin and sample variance by assuming that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upsilon = \infty}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \frac{Z^2_{\alpha/2} s^2}{E^2} }
We want to always round up to stay within the error margin.
I don't really know why.

