Bivariate: Difference between revisions
No edit summary |
m (Admin moved page Two Numerical RVs to Bivariate) |
(No difference)
| |
Revision as of 00:33, 19 March 2024
Consider two numerica random variables and . We can measure their covariance.
The correlation of two random variables measures the line dependent between and
Correlation is always between -1 and 1
Bivariate Normal
The bivariate normal (aka. bivariate gaussian) is one special type of continuous random variable.
is bivariate normal if
- The marginal PDF of both X and Y are normal
- For any , the condition PDF of given is Normal
- Works the other way around: Bivariate gaussian means that condition is satisfied
Predicting Y given X
Given bivariate normal, we can predict one variable given another. Let us try estimating the expected Y given X is x
There are three main methods
- Scatter plot approximation
- Joint PDF
- 5 statistics
5 Parameters
We need to know 5 parameters about and
If follows bivariate normal distribution, then we have
The left side is the predicted Z-score for Y, and the right side is the product of correlation and Z-score of X = x
The variance is given by
Due to the range of , the variance of Y given X is always smaller than the actual variance. The standard deviation is just rooted that.
Regression Effect
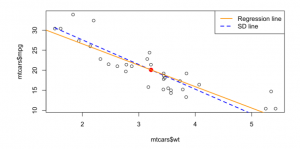
The regression effect is the phenomenon that the best prediction of given is less rare for than ; Future predictions regress to mediocrity.
When you plot all the predicted , you get the linear regression line. The regression effect can be demonstrated by also plotting the SD line (where the correlation is not applied).
Linear Regression
Assumption
- X and Y have a linear relationship
- A random sample of pairs was taken
- All pairs of data are independent
- The variance of the error is constant.
- The average of the errors is zero.
- The errors are normally distributed.
Procedure
where the are regression coefficients (slope, intercept) based on the population, and is error for the i-th subject.
We want to estimate the regression coefficients.
Let be an estimation of ; a prediction at , with
We can measure the vertical error
The overall error is the sum of squared errors . The best fit line is the line minimizing SSE.
Using calculus, we can find that the line has the following scope and intercept:
where is the strength of linear relationship, and is the deviations of the sample. They are basically the sample versions of
Interpretation
(the slope) is the estimated change in when changes by one unit.
(the intercept) is the estimated average of when . If cannot be 0, this may not have a practical meaning.
(coefficient of determination) measures how good the line fits the data.
The bottom is total variance. The top is reduced. The value is the proportion of variance in that is explained by the linear relationship between and .



































