Logistic regression

Figure 1. The shape of the logistic regression function is an S

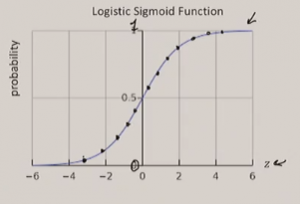
Logistic regression uses the logistic function (sigmoid) to map the output of a linear regression function $z$ to 0 or 1.

Linear regression

Linear regression cannot be directly used for (binary) classification. Indirectly, a threshold is used. When the value is above the threshold, it is considered 1; when it is below, it is considered 0.

Classification using linear regression is sensitive to the threshold. The problem with this approach is the difficulty in determining a good threshold. Logistic regression mitigates that by feeding $z$ into a logistic function.

Logistic function

As shown in figure 1, the sigmoid is S-shaped. It is a good approximation of the transition from 0 to 1.

As stated in the last section, we feed the output of linear regression into sigmoid. Sigmoid outputs a probability of 1.

$sigm(z=wx)={\frac {1}{1+e^{-z}}}$

Decision boundary

The decision boundary is the threshold above which the input can be classified as 1. After the logistic function gives the probability of the event, a decision boundary can be set depending on the scenario.

In normal cases, the decision boundary is set to 0.5. Sometimes, you want to be more than 50% sure before classifying an output to 1. This means shifts to the decision boundary.