Second Order Circuits
Second order circuits are circuits that have two energy storage elements, resulting in second-order differential equations.
There are primarily two types:
- Parallel RLC circuits
- Series RLC circuits
Series RLC Circuits
Unforced
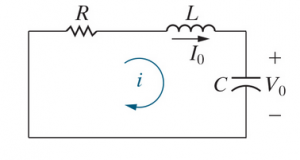
Consider an un-forced RLC circuit. We want to find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_C} .
First, we can use KVL and KCL
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_R + V_L + V_C = 0}
Next, we can use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = C \frac{dV_C}{dt}} and substitution to get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle RC \frac{dV_C}{dt} + L \frac{d}{dt} \frac{C V_C} {dt} V_C = 0}
Changing the order and moving the constants,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LC \frac{d^2 V}{dt^2} + RC \frac{dV_C}{dt} + V_C = 0}
Moving constants away from the first term to get a second-order differential equation,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2V_C}{dt^2} + \frac{R}{L} \frac{dV_C}{dt} + \frac{1}{LC} V_C = 0}
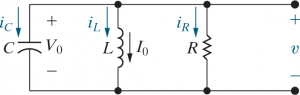
Parallel RLC Circuits
Unforced