Second Order Circuits

Second order circuits are circuits that have two energy storage elements, resulting in second-order differential equations.

One application of second order circuits is in timing computers. As we will see, an RLC circuit can generate a sinusoidal wave.

There are primarily two types of second order circuits:

• Parallel RLC circuits
• Series RLC circuits

Series RLC Circuits

Natural Response

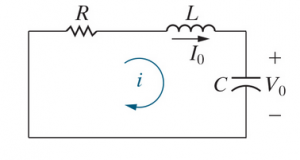An unforced series RLC circuit

Consider an un-forced RLC circuit. We want to find $V_{C}$.

First, we can use KVL and KCL

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_R + V_L + V_C = 0}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle iR + L \frac{di}{dt} + V_C = 0}

Next, we can use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = C \frac{dV_C}{dt}} and substitution to get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle RC \frac{dV_C}{dt} + L \frac{d}{dt} \frac{C V_C} {dt} V_C = 0}

Changing the order and moving the constants,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle LC \frac{d^2 V}{dt^2} + RC \frac{dV_C}{dt} + V_C = 0}

Moving constants away from the first term to get a second-order differential equation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2V_C}{dt^2} + \frac{R}{L} \frac{dV_C}{dt} + \frac{1}{LC} V_C = 0}

Parallel RLC Circuits

Natural Response

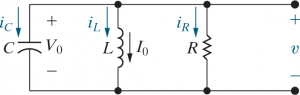A parallel unforced RLC circuit

By KCL,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{v}{R} + \frac{1}{L} \int_0^t v d\tau + I_0 + C \frac{dv}{dt} = 0 }

By differentiating once with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} and rearranging some constants,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2 v}{dt^2} + \frac{1}{RC} \frac{dv}{dt} + \frac{v}{LC} = 0 }

we get a homogeneous second-order differential equation.